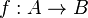Üdvözlök minden látógatot
Sok mindent meg találsz ami kellhet a suliba
A halmazelmélet alapkoncepciói
A halmazelméletben mindent le lehet írni két kifejezéssel. Az egyik a „halmaz” a másik az a kijelentés, hogy egy adott dolog „eleme” egy halmaznak. Ezek a halmazelmélet alapfogalmai.
Tulajdonságok és igazságtartományok
A halmazelmélet legfontosabb objektumai azok a halmazok, melyek egy adott halmaz adott tulajdonságnak eleget tévő elemeiből állnak. Például a természetes számok halmazának, az
halmaznak kiválaszthatjuk azon elemeit, melyek négyzetszámok, azaz előállnak egy természetes szám négyzeteiként:
Amikor valamely szabályosság, vagy tulajdonság teljesül egy halmaz elemeire, akkor ezt az
összetett szimbólummal jelöljük (melyet olyan x-ek a H-ból, melyekre teljesül T(x) -ként mondunk ki) és ahol az ' x ∈ H ' azt jelöli, hogy egy H halmaz elemeiről van szó, a | (függőleges vonal) azt, hogy ezek közül azokat gyűjtjük össze egy halmazba, melyekre igaz a T(x) tulajdonság. Ez lényegében nem más, mint a T tulajdonsg igazságtartománya. A példában eszerint
A végtelen halmazelméleti fogalma
Megjegyezzük, hogy már Galilei is rámutatott, hogy a négyzetszámok „ugyanannyian” vannak, mint a természetes számok. Ezt Cantor a kölcsönösen egyértelmű megfeleltetésekkel fogalmazta meg. Két halmaz azonos számosságú (lényegében azonos elemszámú), ha az egyik halmaz minden elemét hozzárendelhetjük a másik halmaz egy-egy eleméhez olymódon, hogy különbözőkhöz mindig különbözőket rendelünk. Például az n 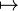 n2 ilyen tulajdonságó, és ekkor a természtes számok és a négyzetszámok egyenlő számosságúak (holott a négyzetszámok a természetes számoknak töredéke).
n2 ilyen tulajdonságó, és ekkor a természtes számok és a négyzetszámok egyenlő számosságúak (holott a négyzetszámok a természetes számoknak töredéke).
Cantor a számosság ezen fogalmával belátta, hogy a természetes számok és a számegyenes pontjai nem azonos számosságúak, azaz nem hozhatók kölcsönösen egyértelmű megfeleltetésbe. A valós számok „sokkal többen vannak” mint a természetes számok. Ez a Cantor-tétel egy variánsa, mely azt a meglepő eredményt közli, hogy nagyon sokféle rendű végtelen van. A végtelen számosságokkal történő számítások a halmazelméletnek máig jelentős része.
A matematika halmazelméleti létrehozása
- Lásd még: rendezett pár, reláció, függvény, rendszám, számosság
A halmazelmélet arra is jó, hogy a matematikai fogalmakat előállítsuk benne. Például a 0 számra gondolhatunk úgy, mint arra a halmazra, melynek egyetlen eleme sincs, azaz az üres halmazra:
Az 1 számra, gondolhatunk úgy, mint egy egyelemű halmazra. A meghatározottság kedvéért legyen 1 az üres halmazt tartalmazó halmaz:
A 2 szám legyen ebből a két halmazból álló halmaz:
És, így tovább, az n-edik természetes szám, az összes halmazelméleti természetes szám halmaza n-ig:
Ezt a konstrukciót Neumann találta ki, Frege és Hume hasonló gondolatainak egyfajta halmazelméleti kivitelezéseként. Sőt ennek mintájára, a sort folytatva Neumann megalkotta a rendszám fogalmát és még Cantor nem csak a véges, de a végtelen számosságfogalmát is.
A halmazelméletben megfogalmazható még a rendezett pár, a függvény, a valós szám és még nagyon sok matematikai fogalmom. Gyakorlatilag az összes.
Túl nagy összességek
A halmazelmélet absztraktságából (tehát hogy csak a „halmaz” és az „eleme” szavakat használja) következnek bizonyos kényelmetlenségek. A kezdetekkor azt gondolták, hogy akármilyen T tulajdonsággal képezhető az { x | T(x) } halmaz és ez is lehet eleme egy halmaznak. Gondolhatunk az { x | x ∉ x } összességre, de valójában az ellentmondás fellépése nélkül nem feltételezhetjük, hogy ez halmaz (lásd: Russell-paradoxon).
A tulajdonságokkal történő halmazképzést tehát korlátozni kell, nem lehet akármilyen dolgokat egy halmazba gyűjteni az ellentmondás fellépése nélkül. Az egyik megoldási mód, ennek a korlátozásnak a kivitelezése, melyet Neumann vitt végig és amiből a Neumann–Bernays–Gödel-halmazelmélet született, ez a méret korlátozásának elve. A másik a halmazok egymás után, műveletek segítségével történő felépítésének útja, melyet iteratív vagy kumulatív elvnek kevezünk, és amit a Zermelo–Fraenkel-halmazelméletben ölt testet.
Halmazműveletek
A halmazok egymásután történő megalkotásának iteratív elve az alábbi úgy nevezett halmazműveleteken nyugszik.
Egyesítés, unió
Ha A és B halmazok, akkor  jelöli azon elemek összességét, melyek A illetve B közül legalább az egyikben benne vannak.
jelöli azon elemek összességét, melyek A illetve B közül legalább az egyikben benne vannak.
Metszet
Ha A, B halmazok, akkor  jelöli a metszetüket, vagy közös részüket, azaz azt a halmazt, ami pontosan A és B közös elemeit tartalmazza. Hasonlóan el lehet készíteni egy akárhány halmazból álló
jelöli a metszetüket, vagy közös részüket, azaz azt a halmazt, ami pontosan A és B közös elemeit tartalmazza. Hasonlóan el lehet készíteni egy akárhány halmazból álló  halmzrendszer elemeinek
halmzrendszer elemeinek  metszetét.
metszetét.
| Idempotencia: |  |
 |
| Kommutativitás: | 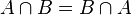 |
 |
| Asszociativitás |  |
 |
| Disztributivitás |  |
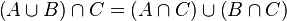 |
Kivonás
Egy A és egy B halmaz különbségét a 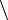 művelettel képezzük, elemei pontosan azok, amelyek elemei A-nak, de nem elemei B-nek:
művelettel képezzük, elemei pontosan azok, amelyek elemei A-nak, de nem elemei B-nek:

Komplementerképzés
Egy A halmaz komplementerét egy adott U alaphalmaz felett értelmezhetjük, definíciója: 
Párképzés
Az a, b elemeket tartalmazó rendezett pár

Ez valóban rendelkezik a rendezett pártól elvárható tulajdonsággal, ugyanis  csak akkor teljesül, ha a=c és b=d.
csak akkor teljesül, ha a=c és b=d.
Descartes-szorzat vagy direkt szorzat
Az A és B halmazok Descartes-féle szorzatán a következő halmazt értjük:

A szorzathalmaz elemei rendezett párok, amely azt jelenti, hogy az elemek közül az első az első halmazból, a második a második halmazból való.
Halmazelméleti függvény
Ha adott az A és B halmaz, akkor az A-n értelmezett és B-be érkező függvénynek nevezzük és
-vel jelöljük, az A×B egy olyan f részhalmazát, mely elemeinek első komponensei között az A összes eleme szerepel és a reláció egyértelmű a második komponensében, tehát
- értelmezési tartománya: Dom( f ) = A, továbbá
- minden egyes x ∈ A elemhez egy és csakis egy olyan y ∈ B-beli elem található, hogy (x, y) ∈ f.
Egy A-beli x-hez tartozó, egyértelműen meghatározott, B-beli y elemet
- f (x)
-szel jelöljük, így y = f (x)  (x, y) ∈ f. Ekkor azt mondjuk, hogy f az x értékhez az y értéket rendeli.
(x, y) ∈ f. Ekkor azt mondjuk, hogy f az x értékhez az y értéket rendeli.
Egy függvényt injektívnek nevezünk, ha különbözőkhöz különbözőket rendel.
Egy f : A  B függvényről azt mondjuk, hogy szűrjektív (vagy ráképez B-re), ha minden elemet felvesz értékként B-ből.
B függvényről azt mondjuk, hogy szűrjektív (vagy ráképez B-re), ha minden elemet felvesz értékként B-ből.
Azt mondjuk, hogy f : A  B bijekció (vagy kölcsönösen egyértelmű, vagy egy-egy értelmű), ha injektív és szűrjektív.
B bijekció (vagy kölcsönösen egyértelmű, vagy egy-egy értelmű), ha injektív és szűrjektív.
Elemi algebra
Elemi algebra az algebra legalapvetőbb alterülete. A számelmélet alapelvein kívül nem szükséges a megértéséhez előzetes matematikai tudás, ezért tanítják igen korán. Számelméletben csak számok és bizonyos aritmetikai műveletek fordulnak elő (mint például az +, -, ×, ÷). Algebrában viszont a számok helyett szimbólumokat használunk (mint a, x, vagy y). Ez azért hasznos, mert:
- Lehetővé teszi a számelméleti törvények általános megfogalmazását (mint a + b = b + a minden a, bre), ami az első lépés az egész számok tulajdonságainak meghatározása felé.
- Lehetővé teszi az "ismeretlen" számokra való utalást, az egyenletek leírását és annak tanulmányozását, hogy hogyan oldhatók meg. (mondjuk "keressük azt az x-et, amire 3x + 1 = 10").
- Végül lehetővé teszi a függvények megalkotását (mint a "ha x jegyet eladunk, a nyereség 3x - 10 Ft lesz" vagyis f(x) = 3x - 10, ahol f a függvény és x az a szám amire alkalmazzuk, meghívjuk.)
Polinomok
A polinomok olyan matematikai kifejezések, amelyek egy vagy több változóból és konstansból állnak továbbá ezek között csak az összeadás, szorzás, kivonás műveleteket használjuk (ahol az ismételt szorzás konstans pozitív egész kitevőjű hatványozással jelölendő). Például a x2 + 2x − 3 egy x változós polinom.
Az algebra egy fontos problémaköre a polinomok faktorizációja, vagyis egy polinom felbontása más polinomok szorzatára. A fenti polinom például (x − 1)(x + 3) alakba írható.
Absztrakt algebra
Az absztrakt algebra az elemi algebrában és számelméletben megtalálható fogalmakat általánosítja, olyan struktúrákat vezetve be, melyek lehetővé teszik absztrakt matematikai fogalmak, kifejezések általános kezelését.
Halmazok: Ahelyett hogy különböző tipusú számokkal foglalkozna, az absztrakt algebra inkább az általánosabb halmaz fogalmát használja. A halmaz olyan azonos tulajdonságú "objektumok" (elemek) "gyűjteménye, mely tulajdonság a halmazra jellemző. Így az összes azonos tipusú szám egy halmazba kerül. A 2×2-es mátrixok halmaza, a másodfokú polinomok halmaza, a kétdimenziós vektorok halmaza több a gyakran használt halmazok közül. Viszont a halmazelmélet a logika és nem az algebra alterülete.
Kétváltozós műveletek: Az összeadás és szorzás általánosítása a kétváltozós művelet fogalma. Ez a fogalom viszont értelmetlen egy halmaz nélkül, amin definiálhatnánk. Ha S halmaz két a és b elemére a*b egy másikat ad meg, akkor a halmazt zártnak nevezzük. Összeadás (+), külünbség (-), szorzás (*) és osztás (÷) mind olyan kétváltozós művelet, ami különböző halmazokon is definiálható, mint például a mátrixok, vektorok, polinomok összeadása és szorzása.
Asszociativitás: Az egész számoknak létezik az a tulajdonsága, hogy tetszőleges csoportokban összeadhatók, például (2+3)+4 = 2+(3+4). Általánosan * művelet asszociativitása (a * b) * c = a * (b * c). Ez a tulajdonság igaz a legtöbb kétváltozós műveletre, de például a kivonásra és osztásra nem.
Egységelem: A nulla és az egy az egységelem triviális példái, előbbi az összeadás, utóbbi a szorzás egységeleme. Általánosan e akkor egységeleme * kétváltozós műveletre, ha a * e = e * a = a. Látható, hogy x + 0 = 0 + x = x és y * 1 = 1 * y = y, de például a pozitív természetes számok halmazán az összeadásnak nincs egységeleme.
Inverz elem: A negatív számok bevezetése teszi lehetővé az inverz fogalmának létrejöttét. Összeadásnál az a inverze a -a, mig szorzásnál az 1/a. Általánosan a-1 akkor inverze a-nak * műveletre, ha a * a-1 = e and a-1 * a = e.
Kommutativitás: Az egészek egy másik tulajdonsága a kommutativitás, hogy tetszőleges sorrendben összeadhatók, és az eredmény nem változik. Általánosan a halmaz elemeire a * b = b * a. Ez a tulajdonság már igen ritka, például jellemző az egészek összeadására és szorzására, de már nem a mátrixok szorzására.
Csoport
A fenti fogalmak segítségével megalkotható a matematika legfontosabb struktúrái közé tartozó csoport. Egy S halmazt és egy hozzá tartozó '*' kétváltozós műveletet akkor nevezünk csoportnak, ha a következő tulajdonságokkal rendelkeznek:
- Létezik e egységelem úgy, hogy minden a elemére az S halmaznak e * a and a * e = a.
- Minden elemnek van inverze, vagyis S minden a elemére található egy a-1 hogy a * a-1 = a-1 * a = e, ahol e a fenti egységelem.
- A művelet asszociatív, vagyis tetszőleges három elemre (a * b) * c = a * (b * c).
Továbbá ha emelett még a művelet kommutatív is az S halmazon a fenti tulajdonságok mellett (a * b = b * a), akkor a csoportot Ábel-csoportnak nevezzünk.
A következő táblázatban néhány példa látható csoportokra és egyéb hasonló algebrai struktúrákra:
| Példák | ||||||||||
| Halmaz: | Természetes számok  |
Egész számok  |
Racionális számok  (hasonlóan a valós (hasonlóan a valós  és komplex és komplex  számok) számok) |
Egészek modulo 3: {0,1,2} | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Művelet | + | × (0 nélkül) | + | × (0 nélkül) | + | − | × (0 nélkül) | ÷ (0 nélkül) | + | × (0 nélkül) |
| Zárt | Igen | Igen | Igen | Igen | Igen | Igen | Igen | Igen | Igen | Igen |
| Egységelem | 0 | 1 | 0 | 1 | 0 | - | 1 | - | 0 | 1 |
| Inverz | - | - | -a | - | -a | - |  |
- | 0,2,1 (megfelelően) | -, 1, 2 (megfelelően) |
| Asszociatív | Igen | Igen | Igen | Igen | Igen | Nem | Igen | Nem | Igen | Igen |
| Kommutatív | Igen | Igen | Igen | Igen | Igen | Nem | Igen | Nem | Igen | Igen |
| Struktúra | monoid | monoid | ábel csoport | monoid | ábel csoport | kvázicsoport | ábel csoport | kvázicsoport | ábel csoport | ábel csoport (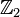 ) ) |
A csoportok elméletért a csoportelmélet vizsgálja. Ezen elmélet legnagyobb eredménye a véges egyszerű csoportok osztályzása, mely az összes véges csoportot közel 30 főbb osztályba sorolja. Ezen munka javát 1955 és 1983 között végezték.
A félcsoport, kvázicsoport és monoid a csoporthoz hasonló, de általánosabb struktúra. A fenti feltételek közül bizonyosakat kielégítenek, bizonyosakat nem. A félcsoportnak például nincs feltétlenül egységeleme, de asszociatív, a monoidnak van egységeleme is, de nincs minden elemnek inverze. A kvázicsoportnál van egy olyan egyváltozós művelet amely egy elemet egy másikhoz rendel hozzá, ugyanakkor a monoidhoz tartozó kétváltozó műveletnek nem kell asszociatívnak lennie. Mindegyik előbbi struktúra speciális esete a grupoidnak, mely egyszerűen halmaz kétváltozós művelettel.
Gyűrű és Test
A csoportokkal ellentétben szükséges olyan struktúrák bevezetése, melyeken egyszerre több művelet is értelmezett. Ezek közül a legfontosabb a gyűrű és a test.
A disztributivitás határozza meg általánosan a két értelmezett művelet viszonyát, sorrendjét. Általánosan (a + b) × c = a×c+ b×c and c × (a + b) = c×a + c×b jelenti azt hogy * disztributív +-ra nézve.
A gyűrű két kétváltozós művelettel is rendelkező halmaz, melyek '+' és '*'. Az első művelet (+) szerint a halmaz ábel csoport, míg a második művelet (*) asszociatív, de nem feltétlenül van egységeleme, illetve inverze. Az additív egységet itt 0-val jelölik, az inverzet -a-val.
A test egy olyan gyűrű, melyen a második művelet szerinti halmaz (a nullát nem számítva) is ábel csoportot alkot. A multiplikatív egységelemet 1-vel jelölik, a multiplikatív inverze a-1.
Az egész számok gyűrűt, míg a racionális, valós és komplex számok testet alkotnak.
GEOMETRIA
A geometria a matematika térbeli törvényszerűségek, összefüggések leírásából kialakult ága; maga a geometria szó görögül eredetileg földmérést jelentett. Kialakulásában és több eredményének felfedezésében nagy szerepet játszott az ókori keleti kollektív munkára épült gazdasági rendszer (innen ered a terület- és térfogatszámítás), és a szintén keleti eredetű, de a görögök által is művelt csillagászat is.
A geometria az i. e. 5. század körül azonban lassan-lassan elszakadt tapasztalati gyökereitől, az eleata filozófusok (leginkább Zénón) és olyan tudósok, mint Thalész hatására. A geometria az első tudományág, amit deduktív módon, vagyis axiómarendszer formájában építettek fel (ez elsősorban Euklidész nevéhez fűződik).
Az axiómákat a görög filozófusoktól eredeztethetően úgy szokás felfogni, mint olyan egyszerű és nyilvánvaló empirikus vagy intuitív tapasztalatok matematikai megfogalmazásait, a tér olyan alapvető tulajdonságait, melyekben épeszű ember nem kételkedik. E felfogás nem alaptalan, de a matematika sok művelője (kutatók, oktatók) mára túlhaladottnak tekinti. Azt mondhatjuk, hogy tulajdonképpen sokkal inkább vagy legalább annyira jellemző a geometriára az, hogy axiomatikus, mint az, hogy a „fizikai” tér leírásával foglalkozna. Ezek a kérdések azonban olyannyira bonyolultak és szerteágazóak, hogy szócikkünk történeti része külön kell hogy foglalkozzon vele. Arra a kérdésre, hogy mi tulajdonképp is a geometria, manapság lehetetlen egy mondatban válaszolni.
Az axiómák segítségével a geometria által vizsgált dolgokkal, például a pontokkal, egyenesekkel, görbékkel, felületekkel és testekkel kapcsolatos logikus következtetések vonhatóak le.
Honlapkészítés ingyen:
Ez a weblapszerkesztő alkalmas
ingyen weboldal,
ingyen honlap készítés...
Mai: 1
Tegnapi: 1
Heti: 1
Havi: 7
Össz.: 10 600
Látogatottság növelés
Üdvözlök minden látógatot - © 2008 - 2026 - bloodsucker.hupont.hu